FlexFlux user documentation

General functioning and file formats

FlexFlux works by taking as an input three different files:

• a file describing the metabolic network (SBML file format [ 1]),
• a constraint file containing the objective function as well as constraints concerning the values of variables,
• a regulation file describing the regulatory network in the SBML-qual [2] file format.

Overview of FlexFlux

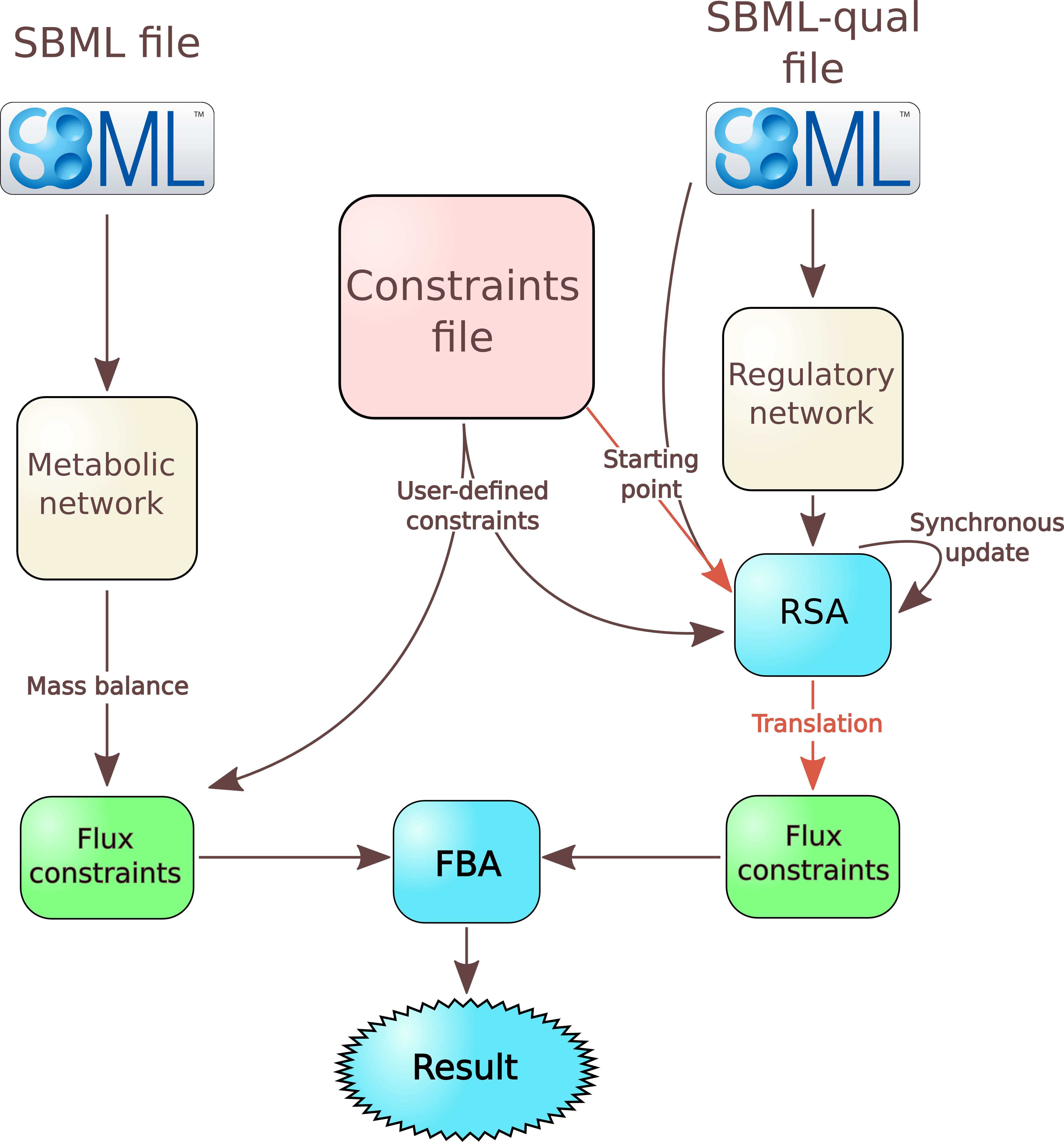
File describing the metabolic network

• it adds to the model all reactions, genes, and proteins as variables;
• consequently to the steady-state assumption, it adds constraints corresponding to the steady state;
• it adds all reaction flux constraints. If no value is given for a reaction, the lower bound is set to 0 for irreversible reactions and to -999999 for reversible ones, and the upper bound is set to 999999;
• it adds to the model all the logical constraints (as interactions) concerning gene-protein-reaction interactions (GPR).

Constraint file

The format of the constraint file is quite similar to existing file formats like the LP file format used by the solver CPLEX.

This file is used to define the objective function as well as constraints.

Objective function

To set the objective function :

obj : MAX(2*a + -1*b)

Nested objective functions

Multiple objective functions can be written. In that case, all objective functions are sequentially considered. The optimal value of an objective function becomes a new constraint (with a percentage of liberty than can be specified) for the following optimization.

Example :

obj : MAX(R_GLC)
obj : MAX(R_BIOMASS)

FlexFlux will first calculate the maximum value for R_GLC, will add it as a constraint, and then will normally continue with R_BIOMASS as the objective function

Constraints

• The line may contain three columns :

  a 3 6
  

  which means 3 < a < 6
• Or two columns :

  b -1
  

  which means b=-1

By default, variables are considered as real numbers (they can take every value between their lower and upper bound, including decimal numbers).

If you don't want your variable to be a real number, you can set as a integer or a binary variable.

To add integer variables, they must be written under the line

INTEGER

INTEGER

a 3 6

For binary values (0 or 1), the variable name has to be written under the line BINARY.

BINARY

a
b 1

Starting points

STARTING POINT

STARTING POINT

allolactose	0
P_lacI	0

Equations

EQUATIONS

• Only one equality (or inequality) is possible by line. For example : 0 < a < 3*b will have to be written over two lines.
• Variables can be written without coefficient. If they have one, it must be placed before the variable name. Exemple 3*a + 4*b < 5.
• The negative sign must be on the coefficient : a+3*-b must be written : a + -3*b.

Equations can be a good way of making a shortcut, for instance :

obj : MAX(a)
 
.....

EQUATIONS
a = R_GLC + -2*R_AC + 3*R_BIOMASS

Example

Example of a constraint file :

obj : MAX(R_BIOMASS)

a 5
c 10
d 0 50
M_glc_D_b 10.4
M_ac_b 0.3

M_lcts_b 5.8

lacZ 0.001 0.03

R_EX_glc_e_ -10.5 999999
R_EX_o2_e_ -15 999999

R_EX_ac_e_ -2.5 4

R_EX_lcts_e_ -3 999999

INTEGER

BINARY

STARTING POINT

allolactose	0
P_lacI	0

EQUATIONS
d = 2*a + 3*c

Regulation file

This file corresponds to the description of a regulatory network with multi-state qualitative variables in the XML based SBML-qual file format.

As decribed in [2], components of the network must be added as qualitativeSpecies by specifying an initial qualitative value and the maximum number of states that this variable can have.
Updates rules for each component are described in the Transition tags : each component has a default value and rules depending on other component states.

FlexFlux uses the given initial values and update rules to update the network state using synchronous update. Once a state that was already found is reached, an attractor has been found. FlexFlux then uses this attractor to create constraints used in the FBA.

FlexFlux allows to translate qualitative states into continuous intervals used as constraints for the FBA. The correspondance between qualitative state and coninutous interval must be specified by the user as a note in the qualitativeSpecies tag.

<qual:qualitativeSpecies qual:id="A" qual:initialLevel="0" qual:maxLevel="2">
	<notes>
		<body xmlns="http://www.w3.org/1999/">
			<p>STATE 0:[0,1[</p>
			<p>STATE 1:]1,4.5]</p>
			<p>STATE 2:]4.5,+inf]</p>
			<p>STATE 3:ND</p>
		</body>
	</notes>
</qual:qualitativeSpecies>

Key words

Getting the summation of all fluxes

The key-word FluxSum can be used to get the sum of the absolute values of all fluxes in the network.

It can be used for instance as an objective function :

obj : MIN(FluxSum)

It can be also used as a constraint :

FluxSum 0 3000

FlexFlux functions

This section details all possible analyses using FlexFlux. FlexFlux can used in two modes:

• Graphical version: GraphicalFlexflux.sh for linux and GraphicalFlexflux.bat for windows (see the installation section). Then choose your options and hit the run button!
• Command line. The arguments are the same. In this documentation, analyses are run in the command line but there is no difference.

  To try the examples of this documentation yourself, you must change the name of the analysis acording to your operating system (see the installation section).

  For example, for windows

  FlexfluxFBA -s ....

  becomes

  Flexflux.bat FBA -s ....

  and for linux it becomes

  ./Flexflux.sh FBA -s ....

The output of all analyses can be either a text file containing all the results data, a graphical representation of the data, or both.

Regulatory steady-state analysis : RSA

Command-line arguments

• -reg String : Regulation file path
• -out String : [OPTIONAL]Output file name
• -cons String : [OPTIONAL]Constraint file path
• -plot : [OPTIONAL, default = false]Plots the results

Example :

FlexfluxRSA -reg regNetwork.xml -plot -out out.txt

Results

• the regulation file lacOperon.sbml,
• the constraints file ConstraintsRSA.txt,
• the command line :

  FlexfluxRSA -reg lacOperon.sbml -cons ConstraintsRSA.txt -out steady_states_result.txt -plot

Steady state analysis result

Entity name	State 1	State 2	State 3	State 4	State 5(Attractor)	Final constraint lower bound	Final constraint upper bound	
EIIAGlc_p	0	0	0	0	0	0.0	0.0	
lacI	1	1	1	1	1	1.0	1.0	
M_lcts_b	3	3	3	3	3	5.8	5.8	
M_glc_D_b	3	3	3	3	3	1.6	1.6	
AMPc	0	1	1	1	1	1.0	1.0	
permease	0	0	0	0	0	0.0	0.0	
lacZ	0	1	0	1	1	1.0	1.0	
CAP	1	1	1	1	1	1.0	1.0	
lacY	0	1	0	1	1	1.0	1.0	
P_lacI	0	1	0	0	0	0.0	0.0	
R_LCTStpp	0	0	0	0	0	0.0	0.0	
EIIAGlc	1	1	1	1	1	1.0	1.0	
betaGal	0	0	1	0	1	1.0	1.0	
R_LACZ	0	0	0	0	0	0.0	0.0	
allolactose	0	1	1	1	1	1.0	1.0

The graphical result :

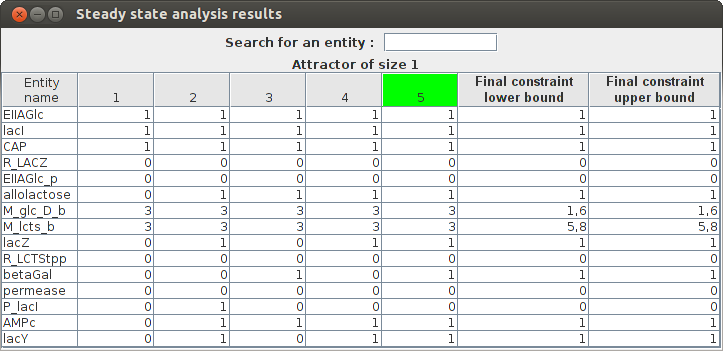
FlexFlux Regulatory steady-state analysis results. The state of the network is updated from the initial values given in the regulation file. The attractor found in shown in green (state 5 here).

Simple FBA

Command-line arguments

• -s String : Sbml file path
• -cons String : Constraint file path
• -reg String : [OPTIONAL] Regulation file path
• -states : [OPTIONAL] The states of the regulatory network are saved in the indicated file name
• -out String : [OPTIONAL]Output file name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -senFile : [OPTIONAL] A sensitivity analysis is performed and saved in the indicated file name
• -h : Prints help

Example :

FlexfluxFBA -s network.xml -cons cons.txt -reg regNetwork.xml -plot -out out.txt

Results

• the SBML file coli.xml,
• the constraint file constraintsFBA_coli.txt,
• the regulation file lacOperon.sbml,
• the command line :

  FlexfluxFBA -s coli.xml -cons constraintsFBA_coli.txt -out FBA_result.txt -reg lacOperon.sbml -plot

FBA result

obj : 0.592258
b2309_and_b2307_and_b2306_and_b2308	Not Constrained
b4031	Not Constrained
b4032	Not Constrained
b4033	Not Constrained
b4034	Not Constrained
R_PANTS	3.41E-4
M_actp_c	Not Constrained
R_G6Ptex	0.0
R_12DGR141tipp	0.0
M_thex2eACP_c	Not Constrained
R_ASCBptspp	0.0
M_tym_p	Not Constrained
R_DXPRIi	0.001415

The graphical result :

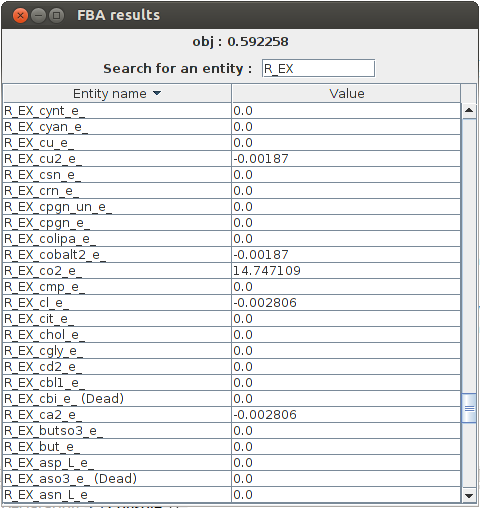
FlexFlux FBA results. In these conditions, given the constraints from the steady state of the regulatory network, the maximum biomass production is 0.592258 and we can see the value of all other variables.

Flux Variability Analyses : FVA

An FVA consists in getting the optimal value for the objective function, setting this value as a constraint and, given a list of entities, minimize and maximize their values. This analysis returns the objective value, and the minimum and maximum value for each entity desired.

The advantage of FlexFlux's FVA compared to classical FVA is that it is not limited to biochemical reactions. It can be done on any variable.

Command-line arguments

• -s String : Sbml file path
• -cons String : Constraint file path
• -reg String : [OPTIONAL]Regulation file path
• -e String : [OPTIONAL]Biological entities to perform the FVA on (Space-separated list of entities, example : "R1 R2 G1 G2"). If empty, FVA is done on all reactions
• -n Integer : [OPTIONAL, default = number of available processors]Number of threads
• -out String : [OPTIONAL]Output file name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -h : Prints help

Example 1 :

FlexfluxFVA -s network.xml -cons cons.txt -reg regNetwork.xml -plot -out out.txt

Example 2 :

FlexfluxFVA -s network.xml -cons cons.txt -reg regNetwork.xml -plot -out out.txt -e "R1 R2 G1 G2" -lib 10

Results

• the SBML file coli_core.xml,
• the constraint file constraintsFBA.txt,
• the command line :

  FlexfluxFVA -s coli_core.xml -cons constraintsFBA.txt -out FVA_result.txt -lib 10 -plot

FVA result

obj : 0.873922(+-10.0%)
Name	min	max
R_CYTBD	35.984865	51.239087
R_PPCK	0.0	17.161
R_PGM	-16.732521	-8.686588
R_Biomass_Ecoli_core_w_GAM	0.786529	0.873922
R_SUCCt3	0.0	22.881333
R_PPC	0.0	20.346866
R_GLNabc	0.0	0.0
R_SUCOAS	-8.045934	0.0
R_CS	0.848587	8.89452
R_EX_glu_L_e	0.0	1.271185
R_EX_akg_e	0.0	1.430083

The graphical result :

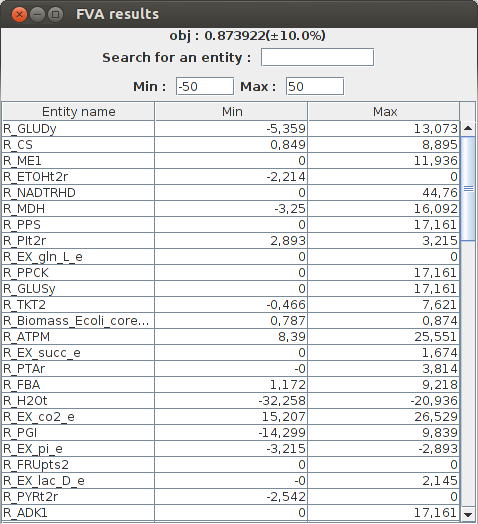
FlexFlux FVA results. Minimum and maximum flux of each reaction for a maximized biomass production (with a liberty of 10%).

Comparison of two FVAs

Command-line arguments

• -s String : Sbml file path
• -cons String : Constraint file path
• -cons2 String : Second constraint file path
• -reg String : [OPTIONAL]Regulation file path
• -e String : [OPTIONAL]Biological entities to perform the FVA analyses on (Space-separated list of entities, example : "R1 R2 G1 G2"). If empty, FVA is done on all reactions
• -n Integer : [OPTIONAL, default = number of available processors]Number of threads
• -out String : [OPTIONAL]Output file name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -h : Prints help

Example 1 :

FlexfluxCompFVA -s network.xml -cons cons.txt -cons2 cons2.txt -reg regNetwork.xml -plot -out out.txt

Example 2 :

FlexfluxCompFVA -s network.xml -cons cons.txt -cons2 cons2.txt -reg regNetwork.xml -plot -out out.txt -e "R1 R2 G1 G2"

Results

• No constraint.
• Constrained glucose uptake.

• the SBML file coli_core.xml,
• the constraint file constraintsFBA.txt,
• a second constraint file constraintsFBA2.txt in witch we allow glucose uptake to be bigger,
• the command line

  FlexfluxCompFVA -s coli_core.xml -cons constraintsFBA.txt -cons2 constraintsFBA2.txt -out comp_FVA_result.txt -lib 5 -plot

FVA comparison result

obj1 : 0.873922(+-5.0%)
obj2 : 1.790569(+-5.0%)
Name	min1	max1	min2	max2
R_EX_succ_e	0.0	0.837122	0.0	1.715171
R_ADK1	0.0	8.5805	0.0	17.5805
R_GLUSy	0.0	8.5805	0.0	17.5805
R_GLUDy	-4.950357	4.265735	-10.142737	8.740022
R_FORt2	0.0	34.322	0.0	70.322
R_FUM	0.792103	7.381819	1.021209	14.146736
R_EX_glc_e	-10.0	-9.523306	-20.0	-19.023306
R_PDH	3.903028	18.770887	6.937593	36.503884
R_GLUt2r	-0.635593	0.0	-1.302259	0.0
R_EX_o2_e	-23.709518	-19.895962	-45.644797	-37.831242

The graphical result :

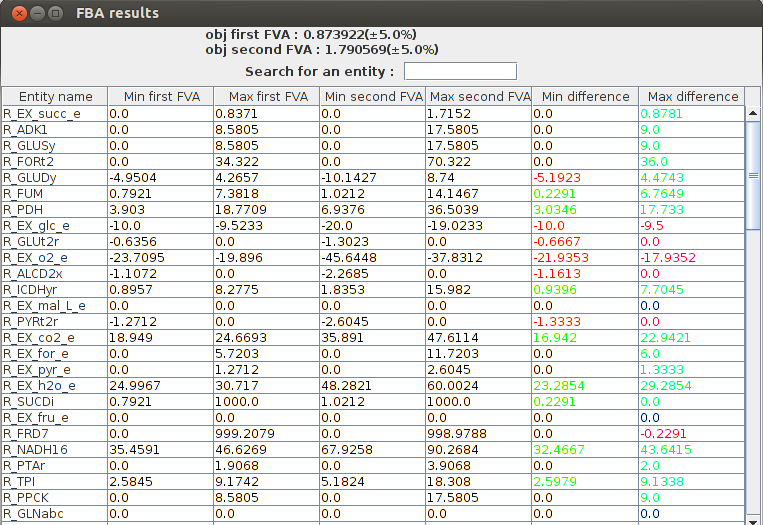
FlexFlux FVA comparison result. We can see the differences between the two conditions. The glucose uptake is bigger in the second case so the biomass production is higher. The two last columns make the comparison between the the FVA's easier. Green values mean the result is higher is the second condition, and red values mean the result is lower in the second condition.

Knock out analysis : KO

• on reactions,
• on genes,
• on any biological entity (specified with argument -e)

Command-line arguments

• -s String : Sbml file path
• -cons String : Constraint file path
• -reg String : [OPTIONAL]Regulation file path
• -e String : [Optional]Biological entities to perform the KO analysis on (Space-separated list of entities, example : "R1 R2 G1 G2"). If empty, KO is done on all reactions (mode 0) or all genes (mode 1)
• -mode Integer : [OPTIONAL, default = 0]KO mode :
  • Mode 0: the KO analysis is performed on reactions.
  • Mode 1: the KO analysis is performed on genes.
• -n Integer : [OPTIONAL, default = number of available processors]Number of threads
• -out String : [OPTIONAL]Output file name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -h : Prints help

Example 1 :

FlexfluxKO -s network.xml -cons cons.txt -reg regNetwork.xml -plot -out out.txt -mode 1

Example 2 :

FlexfluxKO -s network.xml -cons cons.txt -reg regNetwork.xml -plot -out out.txt -e "R1 R2 G1 G2"

Results

• the SBML file coli_core.xml,
• the constraint file constraintsFBA.txt,
• the command line :

  FlexfluxKO -s coli_core.xml -cons constraintsFBA.txt -out KO_result.txt -mode 1 -plot

KO results :

b2277 obj value : 0.211663
b1819 obj value : 0.873922
b3528 obj value : 0.873922
b2296 obj value : 0.873922
b3612 obj value : 0.873922
b2285 obj value : 0.211663
b0720 obj value : 0.0
b2914 obj value : 0.873922

The graphical result :

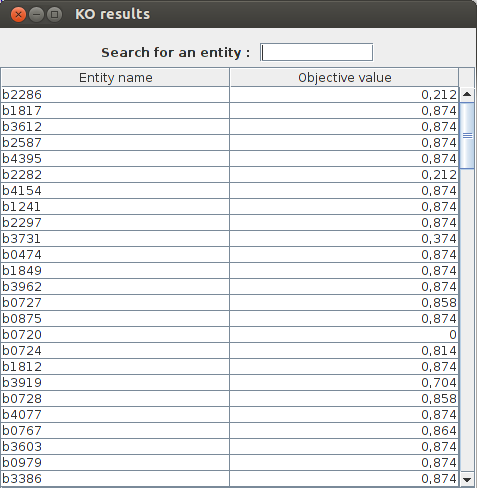
FlexFlux KO analysis result. The analysis is performed on genes because we set the parameter "mode" to 1. We can see what genes are essentials for biomass production. For exemple the gene b0720 is essential because the maximum biomass production is 0 when this gene is knocked out.

Time dependent FBA

This analysis is based on external metabolic concentrations and cell density. Given initial metabolite concentrations, cell density, a time step and a number of iterations, this analysis returns the value of each metabolite and cell density for each time. Initial metabolite concentrations must be written in the constraint file.

Command-line arguments

• -s String : Sbml file path
• -cons String : Constraint file path
• -reg String : [OPTIONAL]Regulation file path
• -e String : [OPTIONAL]Biological entities included in the results. If empty, only concerned metabolites and cell density will be included
• -x Double : Cell density initial value in g/L
• -t Double : [OPTIONAL, default = 0.1]Time between each iteration in hour
• -it Integer : [OPTIONAL, default = 150]Number of iterations
• -bio String : Name of the biomass reaction
• -out String : [OPTIONAL]Output file name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -h : Prints help

Example 1:

FlexfluxTDRFBA -s network.xml -cons cons.txt -reg regNetwork.xml -bio R_BIOMASS -x 0.01 -plot -out out.txt

Example 2:

FlexfluxTDRFBA -s network.xml -cons cons.txt -reg regNetwork.xml -bio R_BIOMASS -plot -out out.txt -x 0.01 -t 0.02 -it 400 -e "R1 R2 G1 G2"

Results

• the SBML file coli.xml,
• the constraint file constraintsFBA_coli.txt where initial concentrations are set,
• the regulation file lacOperon.sbml,
• The command line:

  FlexfluxTDRFBA -s coli.xml -cons constraintsFBA_coli.txt -reg lacOperon.sbml -out TDRFBA_result.txt -bio R_BIOMASS -e lacZ -x 0.011 -plot

The values for this example are extracted from [3] and algorithms for calculations are detailed in [6].

Time	M_lcts_b	lacZ	X	M_glc_D_b	
0.0	5.8	0.0	0.011	1.6	
0.1	5.8	0.0	0.011671	1.592634	
0.2	5.8	1.0	0.012383	1.584819	
0.3	5.8	1.0	0.013139	1.576526	
0.4	5.8	1.0	0.013941	1.567728	
0.5	5.8	1.0	0.014791	1.558393	
0.6	5.8	1.0	0.015694	1.548488	
0.7	5.8	1.0	0.016651	1.53798	
0.8	5.8	1.0	0.017667	1.526829	
0.9	5.8	1.0	0.018745	1.514999	
1.0	5.8	1.0	0.019889	1.502447

The graphical result :

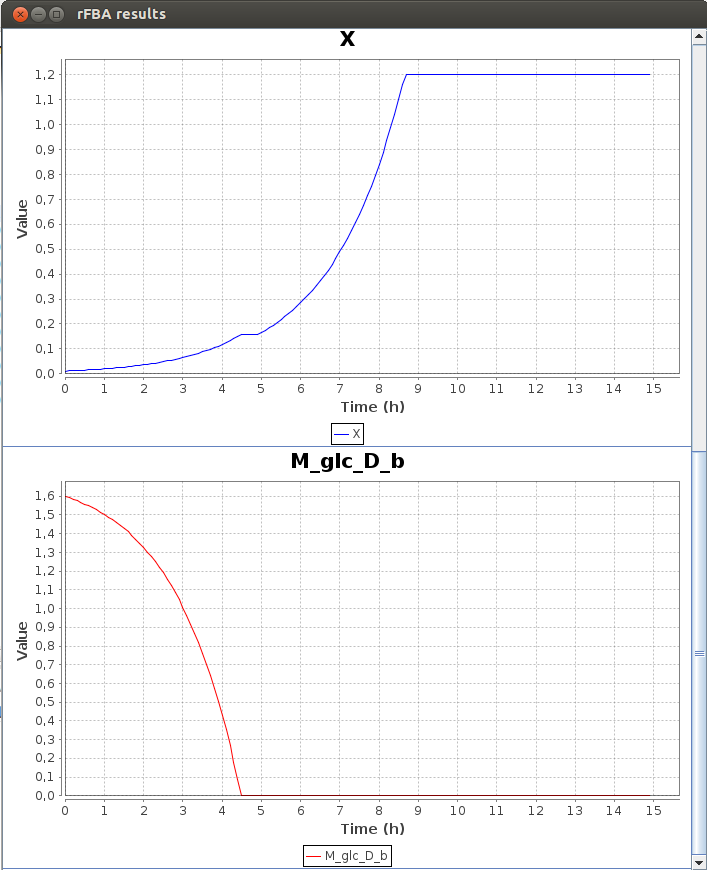
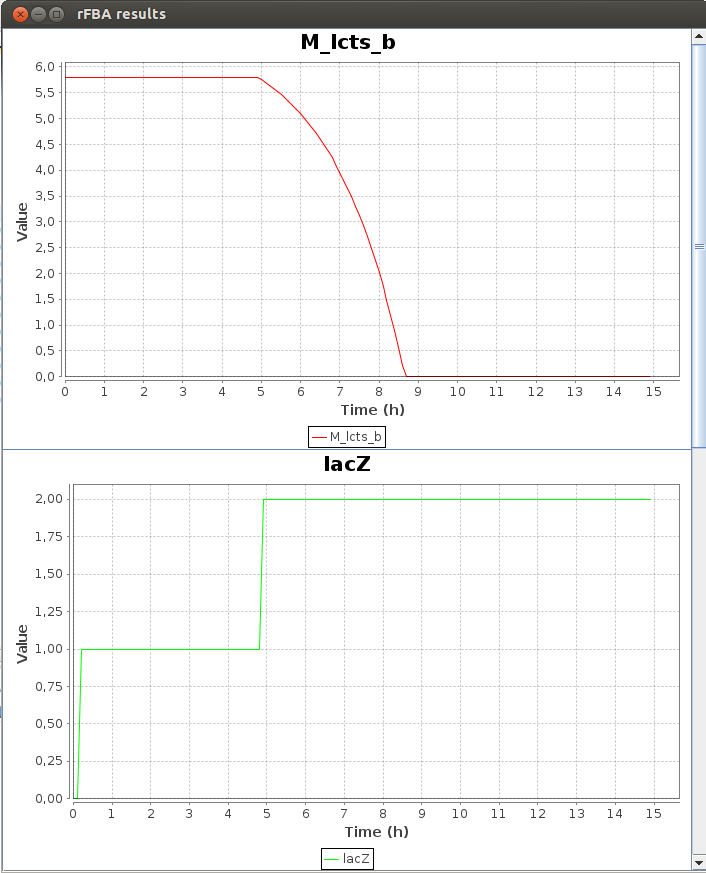
FlexFlux time dependant flux analysis result. We can see the variation of the value of differents entities. X represents the cell density. While the glucose concentration (M_glc_D_b) is greater than 0, the gene lacZ is not activated. When all the glucose is used, lacZ is activated and the cell can use the lactose to grow.

2-D Phenotypic phase analysis

This analysis returns the objective value for each reaction flux.

This permits a phenotype phase plane analysis. [4]

A phenotype phase corresponds to a specific metabolic network behavior.

In order to do that, it calculates the shadow price on each point and groups the points with same shadow price into phenotipic phases that are represented in different colors. To give a hint on what reactions are active in each phase, a FVA is applied on each one and the result is graphically shown: essential reactions are displayed.

Command-line arguments

• -s String : Sbml file path
• -cons String : Constraint file path
• -reg String : [OPTIONAL]Regulation file path
• -r String : Name of the reaction to test
• -init Double : Initial flux value of the reaction to test
• -end Double : Final flux value of the reaction to test
• -f Double : [OPTIONAL, default = 0.1]Difference between each FBA for the reaction flux
• -n Integer : [OPTIONAL, default = number of available processors]Number of threads
• -out String : [OPTIONAL]Output file name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -h : Prints help

Example :

FlexfluxPP2D -s network.xml -cons cons.txt -reg regNetwork.xml -r R1 -init -10 -end 0 -plot -out out.txt

Results

• the SBML file coli_core.xml,
• the constraint file constraintsFBA.txt,
• the command line :

  FlexfluxPP2D -s coli_core.xml -cons constraintsFBA.txt -out PP2D_result.txt -r R_EX_o2_e -init -20 -end 0 -f 0.05 -plot

Reaction flux result

Flux : R_EX_o2_e
Objective : R_Biomass_Ecoli_core_w_GAM

Flux	Objective
-20.0	0.832614
-19.95	0.831466
-19.9	0.830318
-19.85	0.82917
-19.8	0.828023
-19.7	0.825727
-19.75	0.826875

The graphical result :

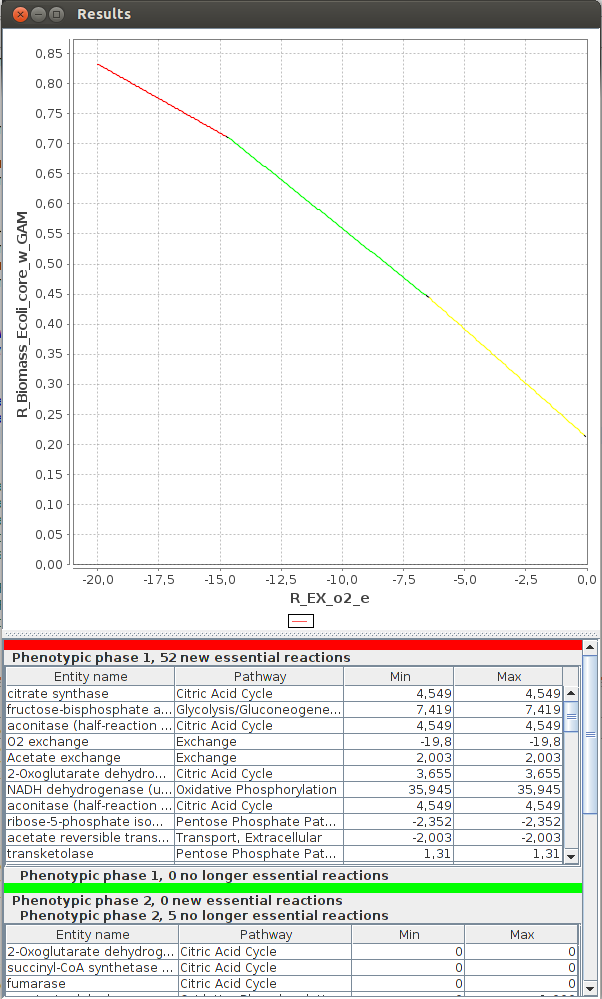
FlexFlux 2-D Phenotypic phase analysis. We can see the evolution of the maximum biomass production for different values of oxygen uptake.

3-D Phenotypic phase analysis

This analysis returns the objective value for each combination of two reaction fluxes.

This permits a phenotype phase plane analysis.

In order to do that, it calculates the shadow price on each point and groups the points with same shadow price into phetotipic phases that are represented in different colors. To give a hint on what reactions are active in each phase, a FVA is applied on each and the result is graphically shown : essential reactions are displayed (the "order" found for the phases is only indicative and might not have any biological meaning).

Command-line arguments

• -s String : Sbml file path
• -cons String : Constraint file path
• -reg String : [OPTIONAL]Regulation file path
• -r String : Name of the first reaction to test
• -r2 String : Name of the second reaction to test
• -init Double : Initial flux value of the first reaction to test
• -end Double : Final flux value of the first reaction to test
• -f Double : [OPTIONAL, default = 0.1]Difference between each FBA for the first reaction flux
• -init2 Double : Initial flux value of the second reaction to test
• -end2 Double : Final flux value of the second reaction to test
• -f2 Double : [OPTIONAL, default = 0.1]Difference between each FBA for the second reaction flux
• -n Integer : [OPTIONAL, default = number of available processors]Number of threads
• -out String : [OPTIONAL]Output file name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -h : Prints help

Example:

FlexfluxPP3D -s network.xml -cons cons.txt -reg regNetwork.xml -r R1 -init -20 -end 0 -r2 R2 -20 -end2 0 -f2 0.2 -plot -out out.txt

Results

• The SBML file coli_core.xml
• The constraint file constraintsFBA.txt
• The command line :

  FlexfluxPP3D -s coli_core.xml -cons constraintsFBA.txt -out PP3D_result.txt -r R_EX_glc_e -init -20 -end 0 -f 0.5 -r2 R_EX_o2_e -init2 -20 -end2 0 -f2 0.05 -plot

Two reactions fluxes result

Flux1 : R_EX_glc_e
Flux2 : R_EX_o2_e
Objective : R_Biomass_Ecoli_core_w_GAM

Flux1	Flux2	Objective
-20.0	-19.5	1.192735
-20.0	-20.0	1.208983
-20.0	-19.0	1.176487
-20.0	-18.5	1.160239
-20.0	-17.5	1.127742
-20.0	-18.0	1.14399
-20.0	-16.5	1.095245
-20.0	-16.0	1.078997
-20.0	-15.5	1.062749
-20.0	-17.0	1.111494
-20.0	-15.0	1.0465

The graphical result :

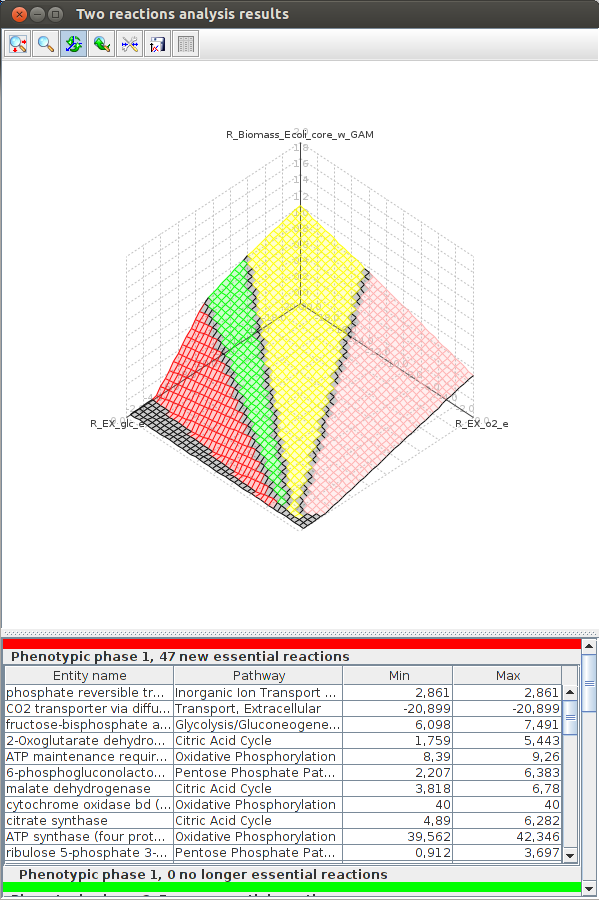
FlexFlux 3-D Phenotypic phase analysis result. We can see the evolution of the maximum biomass production for different values of oxygen and glucose uptake. We observe four distinctive phenotypic phases.

Pareto analysis

The goal of this analysis is to determine what objective (or set of objectives) an organism is optimizing.[5]

It take as an argument a file containing the objective functions to test and experimental values, and finds out (in one, two and three dimensions) what objective optimization is closest to the experimental values.

The objectives that are optimized are those for witch the experimental values are the closest to the pareto surface.

The pareto surface is the surface in which all points are pareto optimal. This means that to increase the value of an objective, you must decrease another.

In this analysis, the objective function of the constraints file is optional and ignored if present.

Objective function and experimental values file

The file must contain all the objectives in the first line, and then one line per experimental value. There must be as many values for one experiment as there are objective functions.

For each experimental value, values for the objectives must be in order and separated by a space.

Example:

MIN(sum) MAX(atpYield) MAX(R_Biomass_Ecoli_core_w_GAM)

1667.4 213.0 6.4
1635.9 191.0 7.9
1622.2 204.0 7.2
1640.4 171.0 7.4
1696.2 176.0 7.2
1657.4 173.0 7.4
1642.9 207.0 6.9
1616.7 185.0 7.7
1569.8 198.0 7.8	

Command-line arguments

• -s String : Sbml file path
• -cons String : Constraint file path
• -reg String : [OPTIONAL]Regulation file path
• -exp String : Path of file containing objective functions and experimental values
• -all : [OPTIONAL, default = false]Plots all results. If false, plots 1D results and only the best result for 2D and 3D results.
• -n Integer : [OPTIONAL, default = number of available processors]Number of threads
• -out String : [OPTIONAL]Output folder name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -h : Prints help

Example : FlexfluxPareto -s network.xml -cons cons.txt -int regNetwork.xml -plot -e expFile

Results

• the SBML file coli_core.xml
• the constraint file constraintsPareto.txt
• the objective/experimental file expFile.txt
• the command line:

  FlexfluxPareto -s coli_core.xml -cons constraintsPareto.txt -exp expFile.txt -out pareto/ -plot

• 1D.txt
• 2D_1.txt
• 2D_2.txt
• 2D_3.txt
• 3D_1.txt

The graphical results :

Axes values are normalized such that the coordinates of the points on the Pareto surface range from 0 to 1, where 1 represents the theoretical minimum or maximum of an objective.

• One dimension
• Two dimensions
• Three dimensions

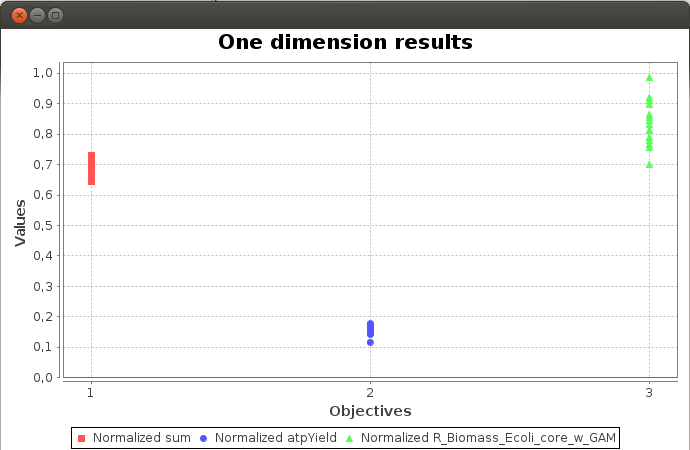
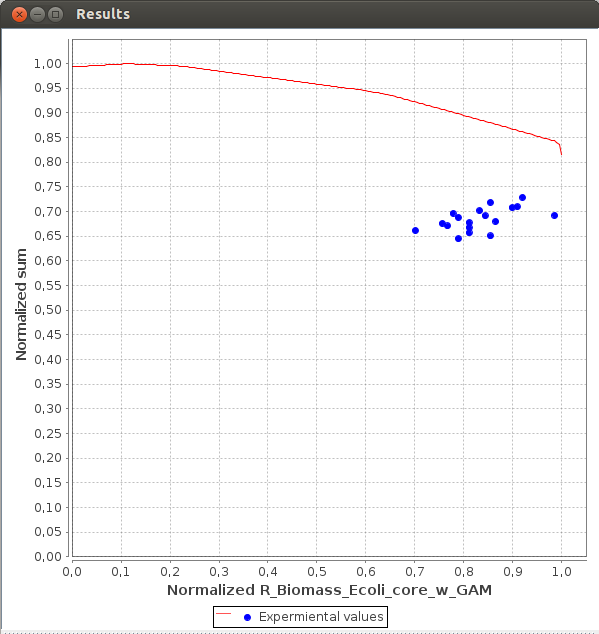
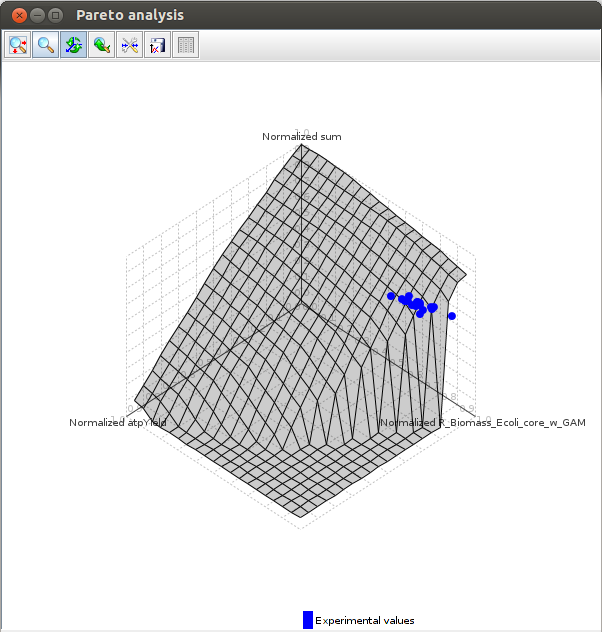
FlexFlux Pareto analysis result.

Dead reactions

Command-line arguments

• -s String : Sbml file path
• -cons String : [OPTIONAL]Constraint file path
• -reg String : [OPTIONAL]Regulation file path
• -d Double : [OPTIONAL, default = 0.000001]Maximal distance of the reaction flux from 0 to be considered as dead
• -mode Integer : [OPTIONAL, default = 0]Dead reactions mode:
  • - Mode 0: Reactions fluxes are not changed.
  • - Mode 1: All reactions fluxes bounds are set to a maximum value. (fluxes become free)
• -n Integer : [OPTIONAL, default = number of available processors]Number of threads
• -out String : [OPTIONAL]Output file name
• -plot : [OPTIONAL, default = false]Plots the results
• -lib Double : [OPTIONAL, default = 0]Percentage of non optimality for new constraints
• -pre Integer : [OPTIONAL, default = 6]Number of decimals of precision for calculations and results
• -sol String : Solver name
• -ext : [OPTIONAL, default = false]Uses the extended SBML format
• -h : Prints help

Example 1 : FlexfluxDR -s network.xml -plot -out out.txt

Example 2 : FlexfluxDR -s network.xml -cons cons.txt -reg regNetwork.xml -plot -out out.txt -mode 1 -d 0.1

Results

• the SBML file coli_core.xml,
• the command line :

  FlexfluxDR -s coli_core.xml -out DR_result.txt -plot

Dead Reactions result

R_EX_fru_e
R_EX_fum_e
R_EX_mal_L_e
R_FUMt2_2
R_GLNabc
R_EX_gln_L_e
R_FRUpts2
R_MALt2_2

The graphical result :

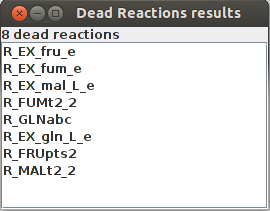
FlexFlux dead reaction identification result. In these conditions, those 8 reactions cannot carry any flux

Biological Entity Clustering by their contribution to the Objective Function (BECO)

Command-line arguments

Input data files

• -s String: Path to the Sbml or MetExploreXml file containing the metabolic network
• -ext: [OPTIONAL, default = false] Uses the MetExploreXml format instead of SBML format for the metabolic network
• -cons String: [OPTIONAL] Constraint file
• -reg String: [OPTIONAL] Path to the regulation file path (SBML-QUAL format)
• -cond String : File describing conditions (set of initial states)
• -o String: Path to the file containing the objective functions
• -out: [OPTIONAL] Path to the output file directory

Parameters for biological entity clustering

• -inchlibPath: Path to the inchlib program [default=/usr/local/inchlib_clust/inchlib_clust.py]
• -mdg: [OPTIONAL] Gene metadata file used for heatmap analysis
• -mdr: [OPTIONAL] Reaction metadata file used for heatmap analysis
• -mdreg File: [OPTIONAL] Regulator metadata file used for heatmap analysis
• -mdSep String: [Default=,] Separator for the columns in the metaData file
• -noGeneAnalysis: Don't perform gene clustering
• -noReactionAnalysis: Don't perform reaction clustering
• -noRegulatorAnalysis: Don't perform regulator clustering
• -fixConditions: [OPTIONAL] If true, the conditions set in the condition file are fixed and can not be updated by the regulation network

Other parameters

• -cytoscape: [OPTIONAL]Generates cytoscape files representing reaction classification for each pair condition/objective
• -plot: [OPTIONAL, default = false] Plots the condition/objective heatmap
• -lib Double: [OPTIONAL, default = 0] Percentage of non optimality for new constraints
• -n Integer: [OPTIONAL, default = number of available processors] Number of threads
• -pre Integer: [OPTIONAL, default = 6] Number of decimals of precision for calculations and results
• -sol Solver: Solver name
• -verbose: [default=false] Activates the verbose mode
• -h: Prints this help

Overview

• Condition and objective clustering
• Reaction clustering
• Metabolic gene clustering
• Regulator clustering
• Metabolic pathway clustering

Results

Condition and objective clustering

Reaction clustering

• Essential reactions
• Zero flux reactions
• Metabolically less efficient (MLE) reactions: enabling not optimal objective flux
• Enzymatically Less Efficient (ELE) reactions: enabling optimal flux but not the minimisation of the flux sum
• Objective Independant Reactions: reactions without effect on the objective function
• pFBA optima reactions: enabling optimal flux an also the minimisation of the flux sum

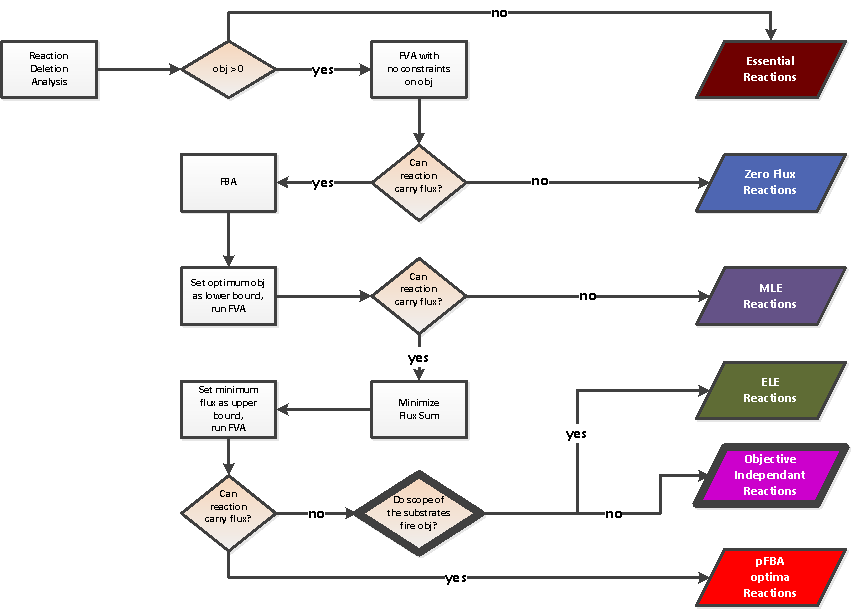
Reaction classification

Metabolic gene clustering

Gene classification algorithm

Regulator clustering

• Essential: if the regulator is inhibited, the optimal value of the objective function is null
• Optimal: if the regulator is inhibited, the optimal value of the objective function is decreased
• Neutral: if the regulator is inhibited, the optimal value of the objective function remains the same